Look, a TeX post again! It’s been another while since I last wrote anything TeX-y here. No wonder, I hardly ever use TeX anymore – but I still do use it from time to time!
A few days ago I needed to draw a diagram of an inclined plane. Interestingly, there are people who did exactly that using TikZ before (obviously), but two examples I found used the heavy artillery of trigonometry. Being a (sort-of) retired mathematician I decided that trigonometry is too hard for me 
and used some TikZ powerful coordinate systems instead. The result is a diagram which is pretty configurable – you can change the actual inclination, for instance, and it Just Works™. So, here’s the code.
\documentclass{article}
\pagestyle{empty}
\usepackage{tikz}
\usetikzlibrary{positioning}
\usetikzlibrary{decorations}
\usetikzlibrary{decorations.pathreplacing}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
\newcommand{\height}{3}
\newcommand{\weight}{2}
\newcommand{\pos}{0.25}
\newcommand{\width}{0.15}
\newcommand{\aspect}{0.67}
% The plane itself
\draw[postaction={
decorate,
draw,
decoration={border,pre length=8pt,segment length=4pt,amplitude=5pt,angle=-135}
}] (0,0) -- (10,0);
\draw (2,0) -- (2,\height) coordinate(top) -- (8,0) coordinate(bot);
% The body on top of it
\coordinate (a) at ($(top)!\pos!(bot)$);
\coordinate (b) at ($(top)!\pos+\width!(bot)$);
\coordinate (c) at ($(b)!\aspect!-90:(a)$);
\coordinate (d) at ($(a)!\aspect!90:(b)$);
\coordinate (m) at ($(a)!0.5!(c)$);
\path (m) ++(0,-\weight) coordinate (n);
\draw (a) -- (b) -- (c) -- (d) -- cycle;
% The weight vector of the body
\draw[->] (m) -- (n);
\path ($(m)+(bot)-(top)$) coordinate (mbot);
\path ($(m)!(n)!(mbot)$) coordinate(m1);
\path ($(m)!(n)!90:(mbot)$) coordinate(m2);
\draw[->] (m) -- (m1);
\draw[->] (m) -- (m2);
\draw[dotted] (m1) -- (n) -- (m2);
\end{tikzpicture}
\end{document}
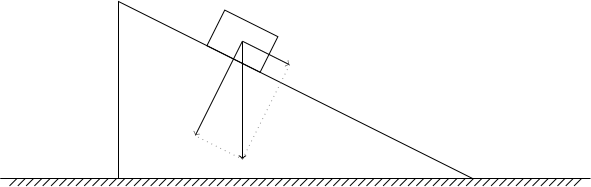
The commands defined at the top are basically variables, defining the height of the inclined plane, the weight of the body, the position of the bottom-left vertex of the body (as a fraction of the plane’s length), its width (the same) and its height (as a fraction of its width). I draw the plane itself first (with a nice ground, using the border decoration) – that is easy enough.
And then, kids, is where it gets complicated. I start with defining the four vertices of the rectangle signifying the body on the plane. The two ones lying on the plane, (a) and (b), are easy. To define (c), I used the so-called partway modifiers. The syntax means that the distance between (a) and (c) will be the given fraction of the distance between (a) and (b), and the line (b) -- (c) will be rotated around (b) by -90° compared to the line (b) --
(a). The point (d) is defined in a similar way.
Then, (m) is the middlepoint of (a) -- (c), and (n) is the other end of the weight vector.
To decompose the (m) -- (n) vector into the two perpendicular components, I used another TikZ coordinate trick – the projection modifiers. It’s very similar to the partway modifiers mentioned before, only now the resulting point is defined not by giving the fraction of the length of a segment, but by a third point – and that third point is projected onto the given segment. So, I first defined the (mbot) point as the (m) point shifted towards the bottom of the plane, in the direction parallel to the plane. This is just a “technical” point we can then use to project (n) onto the line (m) -- (mbot) to get (m1) so that (m) -- (m1) is the component of (m) -- (n) parallel to the plane. The end of the other component vector, the point (m2), os obtained by projection and rotation again – and that’s it!
Interestingly, we completely avoided angle computations (rotation by 90° doesn’t count, ok?). In fact, all the computations involved could be just addition, multiplication and perhaps division (possibly in the form of simple linear algebra). Of course, the rotation part most probably did use some trig functions under the hood, but – since I only rotated by 90° – it didn’t really need to. So, here it is – a diagram of an inclined plane, without trigonometry. Enjoy!